3.2 Infinite impulse response (IIR) filter design
The most commonly used IIR filter design method uses reference analog prototype filter. It is the best method to use when designing standard filters such as low-pass, high-pass, bandpass and band-stop filters.
The filter design process starts with specifications and requirements of the desirable IIR filter. A type of reference analog prototype filter to be used is specified according to the specifications and after that everything is ready for analog prototype filter design.
The next step in the design process is scaling of the frequency range of analog prototype filter into desirable frequency range. This is how an analog prototype filter is converted into an analog filter.
After the analog filter is designed, it is time to go through the last step in the digital IIR filter design process. It is conversion from analog to digital filter. The most popular and most commonly used converting method is bilinear transformation method. The resulting filter, obtained in this way, is always stable. However, instability of the resulting filter, when bilinear transformation is used, may be caused only by the finite word-length side-effect.
3.2.1 Basic concepts and IIR filter specification
First of all, it is necessay to learn the basic concepts that will be used further in this book. You should be aware that without being familiar with these concepts, it is not possible to understand analyses and synthesis of digital filters.
Figure 3-2-1 illustrates a low-pass digital filter specification. The word specification refers to the frequency response specification.
Figure 3-2-1a. Low-pass digital filter specification
Figure 3-2-1b. Low-pass digital filter specification
-
- ωp – normalized passband cut-off frequency;
-
- ωs – normalized stopband cut-off frequency;
-
- δ1 – maximum passband ripples;
-
- δ2 – minimum stopband attentuation;
-
- ε – passband attenuation parameter;
-
- A – stopband attenuation parameter;
-
- ap – maximum passband ripples [dB]; and
-
- as – minimum stopband attenuation [dB].
Frequency normalization can be expressed as follows:
where:
-
- fs is the sampling frequency;
-
- f is the frequency to normalize; and
-
- ω is the normalized frequency.
Specifications for high-pass, band-pass and band-stop filters are defined almost the same way as those for low-pass filters. Figure 3-2-2 illustrates a high-pass filter specification, whereas Figure 3-2-3 illustrates a band-pass filter specification.
Figure 3-2-2a. High-pass digital filter specification
Figure 3-2-2b. High-pass digital filter specification
Comparing these two Figures 3-2-1 and 3-2-2, it is obvious that low-pass and high-pass filters have similar specifications. The same parameters are defined in both cases with the difference that in the later case the passband is substituded by the stopband and vice versa.
Figure 3-2-3 illustrates a band-pass specification.
Filter 3-2-3a. Band-pass digital filter specification
Figure 3-2-3b. Band-pass digital filter specification
Figure 3-2-4 illustrates band-stop digital filter specification
Figure 3-2-4a. Band-stop digital filter specification
Figure 3-2-4b. Band-stop digital filter specification
3.2.2 Z-transform
The Z-transform is performed upon discrete-time signals. It converts a discrete timedomain signal into a complex frequency-domin representation. It is very suitable for analyzing discrete time-domain signals and systems as well. The z-transform is derived from the Fourier discrete time-domain transformation and is considered the basic operation in digital filter design process.
The Z-transform is defined as:
where
z is the complex number.
Example:
Assume that samples of a discrete-time signal x(n) are known. It is necessary to transform this signal with the z-transform and Fourier fransform.
x(n)={1,2,3,4,5,4,3,2,1} ; 0 ≤ n ≤ 8
z-transform is defined via expression:
It becomes:
The last expression is the z-transform of the given signal.
The Fourier transformation can be found by rewriting the previous expression in terms of z as z=e^jω. It becomes:
Figure 3-2-5 illustrates the (frequency) spectrum of the given signal.

Figure 3-2-5. Frequency spectrum of the given signal
Comparing Z and Fourier transforms, it is easy to notice some similarities between them:
In polar coordinates, the complex number z may be expressed as follows:
The two last expressions lead us to the conclusion that Fourier transform is just a special form of the z-transform for
r=1.
In the z plane, the Fourier transform is represented as a unit circle, which can be seen in Figure 3-2-6 below.
Figure 3-2-6. Fourier transform in the z plane
The z-transform of the transfer function is of great importance for IIR filters. The location of poles in the z plane is used for testing stability of designed IIR filter. The poles of the IIR filter transfer function must be located within the unit circle in order that filter is stable.
Figure 3-2-7a illustrates zeros and poles of the transfer function of a stable IIR filter in the z plane.
Figure 3-2-7a Stable IIR filter
Transfer function zeros are denoted by small circles, whereas its poles are denoted by small crosses.
Re – Real axis
Im – Imaginary axis
As seen in Figure 3-2-7, one transfer function zero is located outside the unit circle. It doesn’t cause any problem as the location of poles is the only thing that matters. All four poles of transfer function are located within the unit circle, which guarantees tha stability of IIR filters.
According to the location of poles in the z plane, it is easy to determine whether it refers to FIR or IIR filter. The poles of the FIR filter transfer function are located at the origin. It is obviously not the case in Figure 3-2-7, which means that it refers to IIR, not FIR filter.
Also, Figure 3-2-7a clearly indicates interrelation between zeros and poles in the z plane. If a zero or a pole is located on the real axe in the z plane, i.e. the imaginary part is zero, then it is single. If either of them is not located on the real axis in the z plane, then it has the corresponding pair having the same real value and the same imaginary value with the opposite sign. In the z plane, it is illustrated as a pair of zeros or poles which are symmetric around the real axis. Such a pair is also called a complex-conjugated pair of zeros or poles.
Figure 3-2-7b illustrates the zeros and poles of the transfer function of an instable IIR filter in the z plane.
Figure 3-2-7b. Instable IIR filter
As seen from Figure 3-2-7b, two poles located outside the unit circle make this IIR filter instable. If bilinear transformation is used in the filter design, the resulting filter is stable before the coefficient quantization starts. This quantization changes the location of zeros and poles of the resulting IIR filter, which can cause one pole or one pair of poles to be located outside the unit circle. The result of such a quantization is a filter that is not stable.
3.2.3 Transfer function of discrete-time systems
The Z-transform is primarily used for finding the transfer function of linear discrete-time systems. When the transfer function is found, it is necessary to consider the zeros and poles of the transfer function in the z plane. The transfer function of discrete-time systems is defined to be:
where:
-
- bi are the feedforward filter coefficients (non-recursive part);
-
- aj are the feedback filter coefficients (recursive part);
-
- qi are the zeros of the transfer function;
-
- pj are the poles of the transfer function;
-
- B(z) is the transfer function of non-recursive part of the system; and
-
- A(z) the transfer function of recursive part of the system (feedback).
The recursive part of the transfer function is actually a discrete-time system feedback. Unlike the FIR filters, the IIR filters have feedback which enable them to have greater selectivity as well as nonlinearity of phase characteristic than FIR filters.
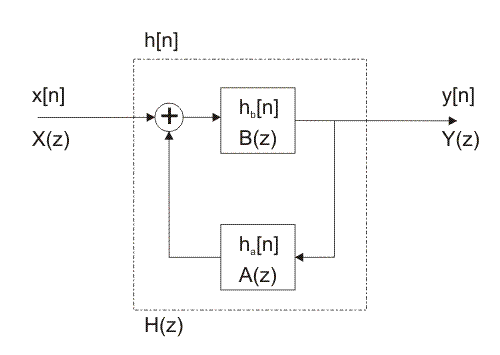
Figure 3-2-8. illustrates block diagram of discrete-time system with feedback.
Figure 3-2-8 Discrete-time system with feedback
In the time domain, the discrete-time system shown in Figure 3-2-8 can be expressed as follows:
OR
The later expression is more convenient for software IIR filters realization.
In the frequency domain, the discrete-time system shown in Figure 3-2-8 can be expressed as the multiplication of Z-transform input signal
X(z) and the transform function
H(z):
The first way of representing discrete-time systems is suitable for both software and hardware IIR filter implementation, whereas the representation in the z domain is suitable for analyzes of designed filters and synthesis itself (design process).
Example:
The transfer function of a 3th order IIR filter, designed using Chebyshev function is:
The following expression describes the filtering process:
This process is also known as convolution. Another expression for convolusion that is more useful in practical applications is:
After making substitutions of impulse response coefficients, it becomes:
Using expression:
it is possible to find function for particular normalized frequency.
For example, when ω = 0.2π:
The numerator is computed first:
Then denominator:
Figure 2-2-8 illustrates a hardware realization of this IIR filter.
Figure 3-2-9. Realization of IIR filter in this example
The software realization would require two buffers each of minimum length 3. One buffer would be used for input samples and another one for output samples. These are usually circular buffers whose length can be expressed as 2^n, which in this case means that the circular buffer is 4 = 2^2 in length.
By complexity, the given IIR filter corresponds to a 6th order FIR filter. Selectivity and attenuation of this filter are much higher than those of any 6th order FIR filter. The result of the feedback, which provides so high selectivity and attenuation, is a non-linear phase characteristic.
3.2.4 Effects of the poles and zeros of the transfer function
The location of poles and zeros of the transfer function is very important for discrete-time system analyses and synthesis. According to their location it is possible to test stability of a discrete-time system, detect round-off errors made due to software implementation of a filter as well as coefficient errors encountered during hardware implementation of a filter.
In order that a discrete-time system is stable, all poles of the discrete-time system transfer function must be located within the unit circle, as shown in Figure 3-2-6. If this requirement is not satisfied, the system becomes unstable, which is very dangerous. The location of zeroes doesn’t affect the stabilty of discrete-time systems. Recalling that FIR flters do not have a feedback, which makes them stable. However, this doesn’t apply on IIR filters. Therefore, it is preferable to use bilinear transformation because it always makes filter stable. In this case, filter stability is questioned only due to coefficient quantization which is performed at the end of the design process.
It always happens due to software and hardware implementation that an error in coefficients representation is produced. In software implementation, an error is triggered by the finite word-length effect, whereas in hardware implementation, it ocurrs due to impossibility of representing the coefficients with apsolute accuracy. The result in both cases is that the actual value of coefficients differs from their value obtained in design process. A direct result of such errors is deviation of the frequency of designed discrete-time system.
Deviation of frequency depends on the spacing between the zeros and poles of the FIR filter transfer function and the origin in the z plane. The FIR filter coefficient error affects more the frequency response as the spacing between the zero and pole of the transfer function and the origin narrows. This property is particularly typical of high-order filters because their zeros are very close each other. Besides, the pole quantization, by rule, affects more frequency characteristic. Slight errors in coefficient representation may cause large frequency deviations.
Figure 3-2-9 illustrates the required and obtained frequency characteristic of an IIR filter. The finite word-length effect on the transform function of an IIR filter is clearly marked in this figure.
Figure 3-2-10. Deviation from required frequency characteristic
The frequency deviation shown in Figure 3-2-10 is basically slight deviation, even though it is very large at certain frequencies. The minimum attenuation and the width of transition region of the resulting IIR filter remain unchanged, so that such deviation is acceptable.
3.2.5 IIR filters design using bilinear transformation
The IIR filter design using bilinear transformation can be split into several steps:
-
- Defining filter specification;
-
- Specifying analog prototype filter;
-
- Computing the filter order required for a given set of specifications and specified analog prototype filter;
-
- Computing the transfer function of reference analog prototype filter;
-
- Conversion into analog filter via scaling;
-
- Conversion into digital filter via bilinear transformation; and
-
- If the obtained filter doesn’t satisfy the given specifications or if it is possible to decrease the filter order, then it is necessary to do it. The filter order can be increased or decreased according to needs and after that steps 4, 5 and 6 are repeated as many times as needed.
The final objective of defining IIR filter specifications is to find the desirable normalized cutoff frequencies (ωc, ωc1, ωc2), transition width, maximum passband attenuation and minimum stopband attenuation. The type of analog prototype filter as well as the filter order will be specified according to these parameters.
Now, it is time to specify the type of reference analog prototype filter. Be aware that every type has its good and bad sides. It is only important that its characteristics can satisfy the given specifications. However, it is preferable to specify such a type of analog prototype filter that can produce the lowest order IIR filter.
After this step, that is, when the type of analog proptotype filter is known, it is necessary to specify or compute the filter order required for a given set of specifications. The initial value of the filter order is roughly estimated and is changed after that depending on the obtained characteristics and requirements.
When both type and order of analog prototype filter are known, it is possible to find its transfer function.
The transfer function of analog prototype filter depends on frequencies which are not scaled into the desirable range. For this reason, it is necessary to perform scaling of the transfer function so that cut-off frequencies go into the desirable range. This operation is actually conversion of reference analog prototype filter into analog filter with desirable characteristic.
Finally, the transfer function of the specified type of reference analog prototype filter is obtained by converting analog filter into digital one. This book represents the most commonly used conversion known as bilinear transformation.
If the resulting filter doesn’t satisfy the given specifications, or if the filter order can be less than actual one, it should be changed. IIR filters have much greater selectivity and attenuation than FIR filters of the same order. For this reason, it is preferable to increase or decrease the filter order by 1. After changing the filter order, the entire IIR filter design process, i.e. computing of the transfer function of reference analog prototype filter, scaling and obtaining analogue filters and conversion into digital filter, is repeated.
3.2.6 IIR filter realization
FIR filter transfer function can be expressed as:
where:
-
- bk the coefficient of non-recursive part of IIR filter; and
-
- ak the coefficient of recursive part (feedback) of IIR filter.
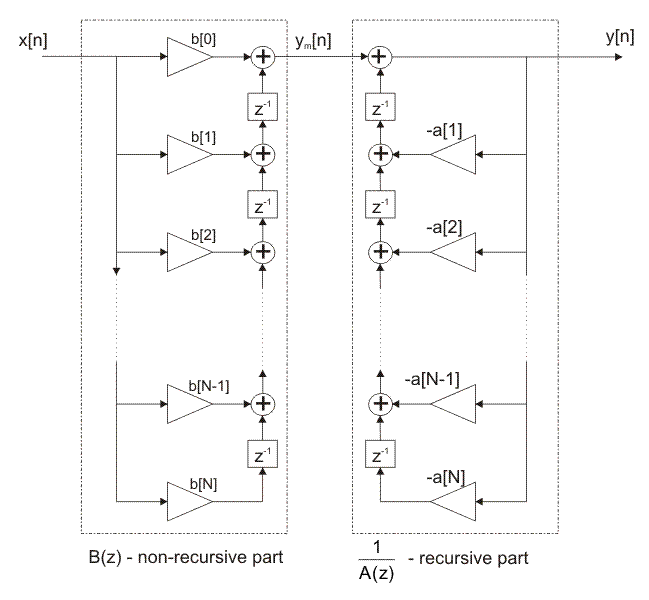
The coefficients bk and ak are of interest for IIR filter realization (both hardware and software). Figure 3-2-11 illustrates the block diagram of IIR filter.
Figure 3-2-11. Block diagram of IIR filter
There are several types of IIR filter realization. This chapter covers direct, direct transpose, direct canonic, direct transpose canonic and cascade realizations. All of them are very convenient and most commonly used for both hardware and software IIR filter realization. Each of them will be described in detail along with their advantages and disadvantages.
3.2.6.1 Direct realization
Direct realization of IIR filters starts with this expression:
The first part of the expression refers to non-recursive part and the other refers to recursive part of IIR filter. In IIR filter direct realization, these two parts are separately considered and realized.
The realization of non-recursive part of IIR filter is identical to the direct realization of FIR filter. Figure 3-2-12. illustrates the block diagram of direct realization of non-recursive part of IIR filter.
Figure 3-2-12. Direct realization of non-recursive part of IIR filter
As seen from Figure 3-2-12 above, multiplication coefficients are identical to those of the transfer function.
Realization of non-recursive part of IIR filter is similar to that of recursive part. Figure 3-2-13. illustrates the direct realization of the filter recursive part.
Figure 3-2-13. Direct realization of non-recursive part of IIR filter
As non-recursive and recursive part of IIR filter are separately realized, it doesn’t matter which of them will be used first in filtering process. Figures 3-2-14a and 3-2-14b illustrate block diagrams of IIR filter realization when non-recursive part is used before and after recursive part of IIR filter, respectively.
Figure 3-2-14a. IIR filter direct realization, non-recursive part is used first
Figure 3-2-14b. IIR filter direct realization, recursive part is used first
This structure is also known as a direct form I structure. As seen from Figures 3-2-14a and 3-2-14b, direct realization requires in total of 2N delay lines, (2N+1) multiplications and 2N additions.
Direct realization is very convenient for software implementation and this is where it is most commonly used. Some of disadvantages of this realization are the greatest sensitivity to accuracy of realized coefficients (i.e. the largest finite word-length effect), and the greatest complexity due to implementation (i.e. needs most resources).
On IIR filter software implementation with direct structure, it is necessary to have two buffers with at least N+1 samples, where N is the IIR filter order. For their simplicity and effectiveness, most commonly used are the so called circular buffers the length of which can be expressed as 2^k. The value of constant k is defined as a minimum value for which N ≤ 2^k is valid. Accordingly:
where the operator
represents rounding down to a less value.
Figure 3-2-15. Circular buffer of length 16 = 2^4
Since the buffer length is 16, location addressing in the circular buffer is performed via module 16 operations:
Example:
A 6th order FIR filter is used in this example. It is necessary to design this filter using direct structure with circular buffer. The length of the buffer needs to be 2^k.
The length of circular buffer is obtained from the following expression:
It means that the minimum length of circular buffer is 2^3 = 8.
The contents of the buffer after receiving the first 10 samples is shown in the table 3-2-1. Input samples are denoted by x[n] and each shaded cell represents changed location in buffer.
| STEP |
ADDR. 7 |
ADDR. 6 |
ADDR. 5 |
ADDR. 4 |
ADDR. 3 |
ADDR. 2 |
ADDR. 1 |
ADDR. 0 |
|---|
| 0 |
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
x[0] |
| 2 |
|
|
|
|
|
|
x[1] |
x[0] |
| 3 |
|
|
|
|
|
x[2] |
x[1] |
x[0] |
| 4 |
|
|
|
|
x[3] |
x[2] |
x[1] |
x[0] |
| 5 |
|
|
|
x[4] |
x[3] |
x[2] |
x[1] |
x[0] |
| 6 |
|
|
x[5] |
x[4] |
x[3] |
x[2] |
x[1] |
x[0] |
| 7 |
|
x[6] |
x[5] |
x[4] |
x[3] |
x[2] |
x[1] |
x[0] |
| 8 |
x[7] |
x[6] |
x[5] |
x[4] |
x[3] |
x[2] |
x[1] |
x[0] |
| 9 |
x[7] |
x[6] |
x[5] |
x[4] |
x[3] |
x[2] |
x[1] |
x[8] |
| 10 |
x[7] |
x[6] |
x[5] |
x[4] |
x[3] |
x[2] |
x[9] |
x[8] |
Table 2-2-2. Input circular buffer after receiving 10 samples
3.2.6.2 Direct transpose realization
Direct transpose realization is similar to direct realization. The only difference is in the position of delay lines, i.e. buffer if it is about software implementation. Here, it is also necessary to have two buffers of minimum length N+1, where N is the filter order.
Figures 3-2-16 and 3-2-17 illustrate the block diagram describing IIR filter direct transpose realization structure of IIR filter.
Figure 3-2-16. IIR filter direct transpose realization, non-recursive part is used first
Figure 3-2-17. IIR filter direct transpose realization, recursive part is used first
There are no significant differences between direct and direct transpose realizations. Both structures have the same multiplication coefficients. The only difference is in the position of delay lines. Similar to direct realization structure, the direct transpose realization structure uses 2N delay lines, (2N+1) multiplications and 2N additions.
3.2.6.3 Direct Canonical Realization
Direct canonical realization structure has reduced number of delay lines to the minimum, that is, N delay lines. This way, one of the main disadvantages of direct and direct transpose realization structures is eliminated. Recursive and non-recursive parts of IIR filter are not considered separately, which causes implementation to be more complex than for direct realization structure. A good thing is that the coefficients are the same as for direct realization.
Figure 3-2-18 illustrates the block diagram describing direct canonic realization structure of IIR filter.
Figure 3-2-18. Direct canonic realization structure block diagram
Similarities between direct canonic structure block diagram and direct realization structure shown in Figure 3-2-14b are obvious. The difference between realization structures shown in Figures 3-2-14b and 3-2-18 is that non-recursive and recursive part for direct canonic realization structure cannot be treated separately, although it is easy to differentiate between them.
Direct canonic structure uses N delay elements, (2N+1) multipilications and 2N additions. Sensitivity to the accuracy of coefficients is the same as for all previously described structures, which is the main disadvantage of this realization structure.
3.2.6.4 Direct transpose canonical realization
Direct transpose canonical realization structure has reduced number of delay lines to the minimum of N delay lines as well as reduced number of adders to N+1. Recursive and nonrecursive parts of IIR filter are not considered separately, which causes implementation to be more complex than for direct realization structure, but similar to direct canonical structure. A good thing is that the coefficients are the same as for direct realization.
Figure 3-2-19 illustrates the block diagram describing direct transpose canonical realization structure of IIR filter.
Figure 3-2-19. Direct transpose canonic realization structure block diagram
Similarities between direct transpose canonical structure block diagram and direct transpose realization structure shown in Figure 3-2-16 are obvious. The difference between realization structures shown in Figures 3-2-16 and 3-2-19 is that non-recursive and recursive part for direct transpose canonical realization structure cannot be treated separately, although it is easy to differentiate between them.
Direct transpose canonic structure uses N delay elements, (2N+1) multipilication elements and N+1 adders. Sensitivity to the accuracy of coefficients is the same as for all previously described structures, which is the main disadvantage of this realization structure.
3.2.6.5 Cascade Realization
Cascade realization structure is the most difficult to obtain from the transfer function (comparing to other realization structures given in this book). It is very convenient for its modular structure and less sensitivity to the accuracy of non-recursive and recursive coefficients realization. On cascade IIR filter realization, a filter is divided into several, mutually independent sections of the first or second order.
Individual sections are mostly realized in direct canonical or direct transpose canonical structure.
Since the sections are mutually independent after design process, the finite word-length effect on the accuracy of coefficients, modulation of frequency response and IIR filter stability are separately examined for each section. The analyse is simplified this way.
The IIR filter transfer function is expressed as:
where:
-
- bi are the coefficients of transfer function numerator (non-recursive part);
-
- aj are the coefficients of transfer function denominator (recursive part);
-
- qi are the zeros of the transfer function;
-
- pj are the poles of the transfer function;
-
- B(z) is the transfer function of non-recursive part;
-
- A(z) is the transfer function of recursive part (feedback); and
-
- M is the number of sections in cascade realization structure.
Cascade realization requires the given expression to be factorized so that the transfer function is expressed as follows:
where:
a[i, k] are the coefficients of recursive part of the i-th IIR filter section;
b[i, k] are the coefficients of non-recursive part of the i-th IIR filter section.
Individual sections are of the first or second order. Direct transpose canonical structure is most frequently used in realization. Figure 3-2-20 illustrates a first-order section.
Figure 3-2-20. First-order section
Figure 3-2-21 illustrates a second-order section.
Figure 3-2-21. Second-order section
The use of direct transpose realization structure reduces necessary number of delay lines and adders as well. Filter dividing in independent sections reduces the sensitivity to the accuracy of quantization coefficients and simplifies analysing the stability of the resulting filter. Besides, the possibility that IIR filter becomes instable after quantization is drastically reduced as the coefficients quantization is performed after dividing filter in sections, so the changes of poles locations are smaller, therefore.
Software realization requires M buffer of length 2 or 1. Each section must have its own buffer for saving samples of intermediate signals. Such complexity and needed factorization are two main disadvantages of this realization structure.
Figure 3-2-21 illustrates the block diagram describing cascade IIR filter structure.
Figure 3-2-22. Cascade IIR filter structure











































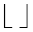 represents rounding down to a less value.
represents rounding down to a less value.